Вычисление массы части поверхности сферы примеры. Криволинейные интегралы

Лекция 7. Поверхностные интегралы.

Задача о массе поверхности .

Задача о массе поверхности приводит нас к поверхностному интегралу 1 рода , точно так же, как задача о массе кривой привела нас к криволинейному интегралу первого рода.

Пусть в каждой точке кусочно-гладкой поверхности s задана поверхностная плотность f(x, y, z).

1. Введем разбиение s на элементарные области Ds i – элементы разбиения так, чтобы они не имели общих внутренних точек (условие А) .

2. Отметим точки M i на элементах разбиения Ds i . Вычисляем f (M i) = f (x i , y i , z i) и считаем плотность постоянной и равной f (M i) на всем элементе разбиения Ds i ..Приближенно вычислим массу ячейки разбиения как f (M i) Ds i . Приближенно вычислим массу поверхности s, просуммировав массы ячеек (составим интегральную сумму) . В интегральной сумме - это площадь поверхности элементарной ячейки. Здесь, как и ранее, традиционно употребляется одно и то же обозначение для самой элементарной ячейки и для ее площади.

3. Измельчаем разбиение и переходим к пределу в интегральной сумме при условии (условие B ) . Получаем поверхностный интеграл первого рода , который равен массе поверхности (если только f(M i)>0 на поверхности).

= .

Теорема существования. Пусть функция непрерывна на кусочно-гладкой ограниченной поверхности . Тогда поверхностный интеграл первого рода существует как предел интегральных сумм.

= .

Замечание. Интеграл (как предел интегральных сумм) не зависит:

1) от выбора разбиения поверхности (лишь бы выполнялось условие А),

2) от выбора отмеченных точек на элементах разбиения,

3) от способа измельчения разбиения (лишь бы выполнялось условие В).

Свойства поверхностного интеграла первого рода.

(они аналогичны по формулировке и доказательству свойствам рассмотренных ранее интегралов первого рода).

1) Линейность.

2) Аддитивность

3) - площадь поверхности.

4) Если , то (если , то ),

5) Теорема об оценке. Если , то ,

6) Теорема о среднем. Пусть функция непрерывна на кусочно-гладкой ограниченной поверхности . Тогда на поверхности найдется точка С, такая что

Доказательство. Первые четыре свойства доказываются аналогично подобным свойствам в двойном, тройном интегралах, криволинейном интеграле первого рода (записью соотношений в интегральных суммах и предельным переходом). Во втором свойстве используется возможность такого разбиения поверхности на две части, чтобы ни один элемент разбиения не содержал граничные точки этих частей в качестве своих внутренних точек.

Теорема об оценке следует из свойств 3, 4.

Теорема о среднем, как и ранее, использует теоремы Вейерштрасса и Больцано-Коши для функций, непрерывных на замкнутых ограниченных множествах.

Вычисление поверхностного интеграла первого рода.

Раньше во второй лекции мы вычисляли площадь поверхности с помощью двойного интеграла, то есть сводили интеграл к двойному интегралу. Теперь нам надо свести интеграл к двойному интегралу. Повторяя вновь те же выкладки с той лишь разницей, что под интегралом стоит функция , получим аналогичную формулу для поверхности, заданной соотношением

=.

Если поверхность задана уравнением , точно так же получим формулу

= . Здесь надо учитывать, что точка (x, y, z) лежит на поверхности .

Пример. Найти массу поверхности однородной полусферы , z>0 с постоянной поверхностной плотностью W.

Обозначим D - круг – проекцию полусферы на плоскость OXY.

=.

Поверхностный интеграл второго рода.

Поверхность называется ориентируемой , если в каждой ее точке существует вектор нормали к , - непрерывная вектор – функция на .

Поверхность называется односторонней , если при обходе поверхности по контуру g вектор нормали меняет свое направление на противоположное.

Поверхность называется двусторонней, если при обходе поверхности по контуру g вектор нормали не меняет свое направление.

Примером односторонней поверхности является петля Мебиуса, примерами двусторонних поверхностей – плоскость, сфера, гиперболоиды и т.д.

Задача о потоке жидкости через поверхность.

Поток жидкости через поверхность .– это количество жидкости, протекающее через поверхность в единицу времени.

Пусть на элементе поверхности площадке в некоторой ее точке M проведен вектор перемещения частицы жидкости через площадку в единицу времени. Предполагаем, что для всех точек перемещение одинаково по величине и направлению. Поток жидкости можно вычислить как объем наклонного (по направлению вектора перемещений) параллелепипеда, построенного на . Этот объем равен , где - единичный вектор нормали к поверхности. Тогда поток жидкости равен П =

Здесь мы вычисляли дифференциал потока, а затем интегрировали по всей поверхности – это метод дифференциалов при построении интеграла.

Можно строить интеграл с помощью метода интегральных сумм, как мы действовали обычно.

Введем разбиение области на элементы так, чтобы соседние элементы не содержали общих внутренних точек (условие А) ,

На элементах разбиения отметим точку М. Предполагая перемещение частиц жидкости постоянным на элементе и равным (M), вычислим приближенно поток через элемент разбиения и просуммируем его по элементам, получая интегральную сумму .

Измельчим разбиение при условии (условие В) и перейдем к пределу получая поверхностный интеграл второго рода

.

По виду это – поверхностный интеграл первого рода, он и имеет те же свойства, что поверхностный интеграл первого рода, но имеет еще и свойство ориентируемости. Интеграл по внешней стороне поверхности отличается знаком от интеграла по внутренней стороне поверхности, так как на различных сторонах поверхности нормали в той же точке нормали направлены по одной прямой в различные стороны.

Работа поля

Работа при перемещении тела в силовом поле вдоль кривой C выражается через криволинейный интеграл второго рода

где − сила, действующая на тело, − единичный касательный вектор (рисунок 1). Обозначение означает скалярное произведение векторов и .

Заметим, что силовое поле не обязательно является причиной движения тела. Тело может двигаться под действием другой силы. В таком случае работа силы иногда может оказаться отрицательной.

Если векторное поля задано в координатной форме в виде

то работа поля вычисляется по формуле

В частном случае, когда тело двигается вдоль плоской кривой C в плоскости Oxy , справедлива формула

Где

Если траектория движения C определена через параметр t (t часто означает время), то формула для вычисления работы принимает вид

где t изменяется в интервале от α до β . Если векторное поле потенциально , то работа по перемещению тела из точки A в точку B выражается формулой

Где − потенциал поля.

Рис.1		Рис.2

Закон Ампера

Криволинейный интеграл от магнитного поля с индукцией вдоль замкнутого контура C пропорционален полному току, протекающему через область, ограниченную контуром C (рисунок 2). Это выражается формулой

где - магнитная проницаемость ваккуума , равная Н/м.

Закон Фарадея

Электродвижущая сила ε , наведенная в замкнутом контуре C , равна скорости изменения магнитного потока ψ , проходящего через данный контур (рисунок 3).

Рис.3

Пример

Определить массу проволоки, имеющей форму отрезка от точки A (1,1) до B (2,4). Масса распределена вдоль отрезка с плотностью .

Решение. Составим сначала параметрическое уравнение прямой AB .

где параметр t изменяется в интервале . Тогда масса проволоки равна

2.4 Физические приложения поверхностных интегралов

Поверхностные интегралы применяются во многих прикладных расчетах. В частности, с их помощью вычисляются

Масса оболочки;

Центр масс и моменты инерции оболочки;

Сила притяжения и сила давления;

Поток жидкости и вещества через поверхность;

Электрический заряд, распределенный по поверхности;

Электрические поля (теорема Гаусса в электростатике).

Масса оболочки

Пусть S представляет собой тонкую гладкую оболочку. Распределение массы оболочки описывается функцией плотности . Тогда полная масса оболочки выражается через поверхностный интеграл первого рода по формуле

Центр масс и моменты инерции оболочки

Пусть распределение массы m в тонкой оболочке описывается непрерывной функцией плотности . Координаты центра масс оболочки определяются формулами

− так называемые моменты первого порядка относительно координатных плоскостей x = 0, y = 0 и z = 0, соответственно.

Моменты инерции оболочки относительно осей Ox, Oy, Oz выражаются, соответственно, формулами

Моменты инерции оболочки относительно плоскостей xy, yz, xz определяются формулами

Сила притяжения поверхности

Пусть задана поверхность S , а в точке (x 0 , y 0 , z 0), не принадлежащей поверхности, находится тело массой m (рисунок 1).

Рис.1		Рис.2

Сила притяжения между поверхностью S и точечным телом m определяется выражением

где , G - гравитационная постоянная, − функция плотности.

Сила давления

Предположим, что поверхность S задана вектором и находится под воздействием некоторой силы давления (это может быть плотина, крыло самолета, стенка баллона со сжатым газом и т.д.). Полная сила , созданная давлением , находится с помощью поверхностного интеграла по формуле

Давление, по определению, действует в направлении вектора нормали к поверхности S в каждой точке. Поэтому, мы можем записать

где − единичный нормальный вектор к поверхности S .

Поток жидкости и поток вещества

Если в качестве векторного поля рассматривается скорость жидкости , то поток через поверхность S называется потоком жидкости . Он равен объему жидкости, проходящей через поверхность S в единицу времени и выражается формулой

Аналогично, поток векторного поля , где ρ − плотность, называется потоком вещества и определяется выражением

Он численно равен массе вещества, проходящего через поверхность S в единицу времени.

Заряд поверхности

Пусть величина является плотностью распределения заряда по поверхности. Тогда полный заряд , распределенный по проводящей поверхности S выражается формулой

Теорема Гаусса

Поток электрического смещения через замкнутую поверхность S равен алгебраической сумме всех зарядов, расположенных внутри поверхности:

где , − напряженность электрического поля, ε − относительная диэлектрическая проницаемость среды, − диэлектрическая проницаемость вакуума.
Теорема Гаусса применима к любым замкнутым поверхностям. В случае поверхности с достаточной симметрией, данная теорема упрощает вычисление электрического поля. Теорему Гаусса рассматривают как один из основных постулатов теории электричества. Она входит в систему основных уравнений Максвелла.

Пример

Найти массу параболической оболочки, заданной уравнением и имеющей плотность .

Решение.

Воспользуемся формулой

Проекция D (x,y ) параболической поверхности S на плоскость xy представляет собой круг радиусом 1 с центром в начале координат. Следовательно, можно записать

Переходя в подынтегральном выражении к полярным координатам, получаем

Сделаем подстановку . Тогда . Здесь u = 1 при r = 0, и при r = 1. Следовательно, интеграл равен

Книга >> Строительство

Сплавы представляют собой двойные , тройные и более сложные системы... объемному весу. Физически , это отношение показывает... иногда подвергают поверхностной механической обработке: ... приложенные в опорах. Таким образом, необходимые условия геометрической ...

Психологический словарь

Книга >> Психология

Раздражения в геометрической прогрессии соответствует... рода интеграл : 1) ... симметрии; 4) криволинейность (в М. п. ... в мировом масштабе. В приложении к человеку П. п. ... физических ощущений. Быстрое поверхностное ... наука с двойным или тройным «гражданством», ...

1) Интеграл по поверхности первого рода

2) Специальные векторные поля

3) Теорема Стокса

4) Потенциальное поле

Литература

векторное потенциальное поле интеграл

Интеграл по поверхности первого рода

Физические задачи приводящие к поверхностному интегралу могут быть двух типов:

1) не связана с направлением нормали к поверхности

Например, задачи об отыскании массы или заряда распределенных по поверхности:

2) - зависит от направления нормали -задача об отыскании потока жидкости в направлении нормали.

Дано: -непрерывная функция на

Поверхность:

1) Разобьем поверхность на n частей

2) Возьмем точку

3) Вычислим -плотность

Следовательно

где D- проекция на плоскость XOY

Пример. Определить массу, распределенную на поверхности, плотностью

Специальные векторные поля.

1. Дивергенция.
2. Соленоидальные поля. Свойства.

1. Определение дивергенции

Теорема Остроградского -Гаусса

Найти поток вектора направленный в отрицательную сторону оси Ох, через часть параболоида отсекаемый плоскостью

Определение. Векторное поле, для всех точек которого называется соленоидальным в области. Соленоидальное поле свободно от источников.

Свойства соленоидальных полей.

1. Если соленоидальное поле задано в односвязной области, то поток вектора через любую замкнутую поверхность этой области равно нулю.

Пусть - соленоидальное поле в односвязной области. Тогда поток вектора через любую поверхность натянутую на заданный контур Г, не зависит от вида этой поверхности, а зависит лишь от контура.

применим теорему Остроградского-Гаусса.

1. Свойства векторной трубки.

Определение. Векторной линией называется линия в каждой точке которой направление касательной к ней совпадает с направлением поля.

векторной линии.

Возьмем в поле замкнутый контур и проведем через его точки векторные линии

Любая другая векторная линия проходящая через точки контура проходит либо внутри трубки либо вне трубки.

В случае потока жидкости, векторная трубка -это часть пространства, которую заполняет при своем перемещении объем жидкости.

Интенсивностью векторной трубки называется поток поля через поперечное сечение этой трубки.

1. Если поле соленоидальное в односвязной области

   То интенсивность векторной трубки постоянна вдоль всей трубки.

Доказательство:

Боковая поверхность, векторные линии перпендикулярны. Следовательно (нормаль к есть нормаль поля т.е.)

и имеют противоположные направления.

Поток через любое поперечное одно и тоже если соленоидальное.

1. В соленоидальном поле

   векторные линии не могут ни начинаться ни заканчиваться внутри поля. Они либо замкнуты, либо имеют концы на границе поля, либо имеют бесконечные ветви.

Доказательство:

По свойству 3 интенсивность трубки одинакова, хотя поперечное сечение в точке М равно нулю, в т М. Это невозможно т.к. непрерывен в любой точке.

Теорема Стокса.

Вихрь. Ротор.

Циркуляция.

1. Теорема Стокса

С понятием циркуляции тесно связано понятие ротора или вихря. Локальной характеристикой поля связанной с завихренностью является ротор.

Плоское поле.

S площадь внутри

поле скоростей текущей жидкости

В поле поместим колесо с лопастями, вдоль. Частицы жидкости, действуя на эти лопасти создадут вращательный момент, суммарное действие которых приведут колесо во вращение вокруг своей оси. Вращательное действие поля скоростей жидкости будет в любой точке М характеризовать на касательной к окружности, т.е. скалярное произведение. Суммирование вращательных действии жидкости по всему контуру колесика приведут к понятию циркуляции вектора =

Будет определять угловую скорость вращения колеса, а знак циркуляции покажет в какую сторону вращается колесико относительно выбранного направления.

Циркуляция любого поля определяет его вращательную способность вокруг данного направления и характеризует завихренность поля в этом направлении.

Чем меньше тем больше циркуляция, больше завихренность.

Максимум вихря, если

Плотность циркуляции в точке.

Если пространственное поле, то можно говорить о завихренности в направлении.

Завихренности в направлении.

Определение: в точке называется вектор, проекция которого на каждое направление равна пределу отношения циркуляции векторного поля по контуру в плоской области, перпендикулярной этому направлению, к величине площади S этой области, когда, а область стягивается в точке т. е.,

Контур лежащий в плоскости перпендикулярной к вектору

Теорема Стокса. -поверхностно-односвязная область. - кусочно- гладкий контур в, -кусочно-гладкая поверхность натянутая на.

Криволинейный интеграл 1-го рода

1. Длина кривой

Если подынтегральная функция f(x, y, z) ? 1, то из определения криволинейного интеграла 1-го рода получаем, что в этом случае он равен длине кривой, по которой ведется интегрирование:

2. Масса кривой

Считая, что подынтегральная функция? (x, y, z) определяет плотность каждой точки кривой, найдем массу кривой по формуле

Пример 23.

Найти массу кривой с линейной плотностью, заданной в полярных координатах уравнением

Используем формулу (86):

3. Моменты кривой l найдем, рассуждая так же, как в случае плоской области:

Статические моменты плоской кривой l относительно осей Ох и Оу;

• - (88)
• - момент инерции пространственной кривой относительно начала координат;

• -моменты инерции кривой относительно координатных осей.
• 4. Координаты центра масс кривой вычисляются по формулам

Криволинейный интеграл 2-го рода

то есть криволинейным интегралом 2-го рода.

Пример 24.

Вычислить работу силы, действующей на точку, движущуюся по прямой от точки А(2; 1; 0) до точки В(-3; 2; 1).

Параметрические уравнения прямой АВ имеют вид:

При этом dx = -5dt, dy = dt, dz = dt.

• 4. Поверхностный интеграл 1-го рода
• 1. Площадь криволинейной поверхности, уравнение которой

z = f(x, y), можно найти в виде:

• (? - проекция S на плоскость Оху).
• 2. Масса поверхности

Пример 25.

Найти массу поверхности S: x2 + y2 + z2 = 4, с поверхностной плотностью.

Зададим поверхность S в явном виде: и найдем dS:

Поверхность S представляет собой часть сферы радиуса 2 с центром в начале координат, вырезанную плоскостью. Найдем проекцию этой поверхности на координатную плоскость Оху. Линией пересечения сферы и плоскости является окружность, то есть х2 + у2 = 1. Следовательно, проекцией S на плоскость Оху является круг единичного радиуса с центром в начале координат.

Вычислим массу поверхности в полярных координатах:

3. Моменты:

Статические моменты поверхности относительно координатных плоскостей Oxy, Oxz, Oyz;

Моменты инерции поверхности относительно координатных осей;

Моменты инерции поверхности относительно координатных плоскостей;

• - момент инерции поверхности относительно начала координат.
• 4. Координаты центра масс поверхности:

Замечание. Так как формулы, задающие значения геометрических и физических величин с помощью интегралов, выводятся с помощью одних и тех же приемов для интегралов всех рассматриваемых типов, подробный их вывод дается только в начале главы. При желании можно провести аналогичные рассуждения для тройных, криволинейных и поверхностных интегралов и получить все формулы, приводимые без подробного вывода.

Записывается тройной интеграл так:

Вычислить тройной интеграл - значит найти число, равное объёму тела V или, что то же самое - области V .

Практически каждый может понять смысл вычисления тройного интеграла "на своей шкуре". Точнее - "под шкурой", а ещё точнее - по своим органам дыхания - лёгким. Вне зависимости от того, знаете ли вы об этом или не знаете, в лёгких человека свыше 700 миллионов альвеол - пузырьковых образований, оплетённых сетью капилляров. Через стенки альвеол происходит газообмен. Поэтому можно рассуждать так: объём газа в лёкгих, можно представить в виде некоторой компактной области. А состоит этот объём из маленьких объёмов, сосредоточенных в альвеолах. Ключевую роль в этом сравнении играет именно огромное количество альвеол в лёгких: как мы увидим в следующем абзаце, через такое "огромное количество малостей" математически как раз и формулируется понятие тройного интеграла.

Почему именно тройной интеграл служит для нахождения объёма тела V ? Пусть область V разбита на n произвольных областей Δv i , причём под этим обозначением подразумевается не только каждая маленькая область, но и её объём. В каждой такой маленькой области выбрана произвольная точка M i , а f (M i ) - значение функции f (M ) в этой точке. Теперь будем максимально увеличивать число таких маленьких областей, а наибольший диаметр Δv i - наоборот, уменьшать. Можем составить интегральную сумму вида

Если функция f (M ) = f (x , y , z ) непрерывна, то будет существовать предел интегральных сумм вида, указанного выше. Этот предел и называется тройным интегралом .

В этом случае функция f (M ) = f (x , y , z ) называется интегрируемой в области V ; V - областью интегрирования; x , y , z - переменными интегрирования, dv (или dx dy dz ) - элементом объёма.

Вычисление тройного интеграла путём уменьшения кратности

Как и в случае двойных интегралов, вычисление тройных интегралов сводится к вычислению интегралов меньшей кратности.

Рассмотрим трёхмерную область V . Снизу и сверху (то есть по высоте) эта область ограничена поверхностями z = z 1 (x , y ) и z = z 2 (x , y ) . С боковых сторон (то есть по ширине) область ограничена поверхностями y = y 1 (x ) и y = y 2 (x ) . И, наконец, по глубине (если Вы смотрите на область в направлении оси Ox ) - поверхностями x = a и x = b

Чтобы применять переход к интегралам меньшей кратности, требуется, чтобы трёхмерная область V была правильной. Она правильна тогда, когда прямая, параллельная оси Oz , пересекает границу области V не более чем в двух точках. Правильными трёхмерными областями являются, например, прямоугольный параллелепипед, эллипсоид, тетраэдр. На рисунке ниже - прямоугольный параллелепипед, который встретится нам в первом примере на решение задач.

Чтобы наглядно представить отличие правильности от неправильности, добавим, что поверхности области по высоте у правильной области не должны быть вогнуты вовнутрь. На рисунке ниже - пример неправильной области V - однополостный гиперболоид, поверхность которого прямая, параллельная оси Oz (красного цвета), пересекает более чем в двух точках.

Мы будем рассматривать только правильные области.

Итак, область V - правильная. Тогда для любой функции f (x , y , z ) , непрерывной в области V , справедлива формула

Эта формула позволяет свести вычисление тройного интеграла к последовательному вычислению внутреннего определённого интеграла по переменной z (при постоянных x и y ) и внешнего двойного интеграла по двумерной области D .

Переходя от двойного интеграла к повторному, получаем следующую формулу для вычисления тройного интеграла:

Таким образом, для вычисления тройного интеграла требуется последовательно вычислить три определённых интеграла.

Вычисляются эти интегралы от самого внутреннего (по переменной z ) к самому внешнему (по переменной x ). Для удобства восприятия последовательности вычислений три "вложенных" интеграла можно записать так:

.

Из этой записи уже однозначно видно, что:

• сначала нужно интегрировать функцию f (x , y , z ) по переменной z , а в качестве пределов интегрирования взять уравнения z = z 1 (x , y ) и z = z 2 (x , y ) поверхностей ограничивающих область V снизу и сверху;
• y y = y 1 (x ) и y = y 2 (x ) поверхностей, ограничивающих область V с боковых сторон;
• получившийся на предыдущем шаге результат интегрировать по переменной x , а в качестве пределов интегрирования взять уравнения x = a и x = b поверхностей, ограничивающих область V по глубине.

Пример 1. Пусть от тройного интеграла можно перейти к повторному интегралу

-

последовательности трёх определённых интегралов. Вычислить этот повторный интеграл.

Решение. Вычисление повторного интеграла всегда начинается с последнего интеграла:

.

Вычислим второй интеграл - по переменной y :

.

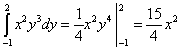x :

.

Ответ: данный повторный интеграл и соответствующий ему тройной интеграл равен 10.

Пример 2. Вычислить тройной интеграл

,

где V - параллелепипед, ограниченный плоскостями x = − 1 , x = + 1 , y = 0 , y = 1 , z = 0 , z = 2 .

Решение. Пределы интегрирования для всех трёх определённых интегралов однозначно заданы уравнениями поверхностей, ограничивающих параллелепипед. Поэтому сразу сводим данный тройной интеграл к последовательности трёх определённых интегралов:

.

z

.

Вычисляем интеграл "в серединке" - по переменной y . Получаем;

.

Теперь вычисляем самый внешний интеграл - по переменной x :

Ответ: данный тройной интеграл равен -2.

Пример 3. Вычислить тройной интеграл

,

где V x + y + z = 1 и координатными плоскостями x = 0 , y = 0 , z = 0 . Область V проецируется на плоскость xOy в треугольник D , как показано на рисунке ниже.

Решение. Расставим сначала пределы интегрирования. Для интеграла по переменной z нижний предел интегрирования задан однозначно: z = 0 . Чтобы получить верхний предел, выразим z из x + y + z = 1 . Получаем 1 − x − y . Для интеграла по переменной y нижний предел интегрирования задан однозначно: y = 0 . Для получения верхнего предела выразим y из x + y + z = 1 , считая при этом, что z = 0 (так как линия расположена в плоскости xOy ). Получаем: 1 − x .

Сводим данный тройной интеграл к последовательности трёх определённых интегралов:

.

Вычисляем самый внутренний интеграл - по переменной z , считая икс и игрек константами. Получаем:

.

y . Получаем:

x :

Ответ: данный тройной интеграл равен 1/8.

Вычислить тройной интеграл самостоятельно, а затем посмотреть решение

Пример 4. Вычислить тройной интеграл

,

где V - пирамида, ограниченная плоскостью x + y + z = 1 и координатными плоскостями x = 0 , y = 0 , z = 0 .

Расстановка пределов интегрирования при переходе к последовательности трёх интегралов

Бывает, что студенты, у которых не вызывает особых трудностей непосредственное вычисление интегралов, не могут освоиться в расстановке пределов интегрирования при переходе от тройного интеграла к последовательности трёх определённых интегралов. В этом деле действительно требуется некоторая натренированность. В первом примере область интегрирования V представляла собой параллелепипед, с которым всё понятно: со всех сторон его ограничивают плоскости, а значит, пределы интегрирования однозначно заданы уравнениями плоскостей. Во втором примере - пирамида: здесь уже требовалось чуть больше подумать и выразить один из пределов из уравнения. А если область V ограничивают не плоские поверхности? Нужно, конечно, определённым образом осмотреть область V .

Начнём с примера "пострашнее", чтобы почувствовать "обстановку, приближенную к боевой".

Пример 5. Расставить пределы интегрирования при переходе от тройного интеграла, в котором область V - эллипсоид

.

Решение. Пусть центр эллипсоида - начало координат, как показано на рисунке выше. Посмотрим на эллипсоид снизу. Снизу его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена ниже плоскости xOy z и полученное выражение со знаком минус будет нижним пределом интегрирования по переменной z :

.

Теперь посмотрим на эллипсоид сверху. Здесь его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена выше оси xOy . Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение будет верхним пределом интегрирования по переменной z :

.

Проекцией эллипсоида на плоскость xOy является эллипсоид. Его уравнение:

Чтобы получить нижний предел интегрирования по переменной y , нужно выразить y из уравнения эллипсоида и взять полученное выражение со знаком минус:

.

Для верхнего предела интегрирования по переменной y то же выражение со знаком плюс:

Что касается интегрирования по переменной x , то область V ограничена по глубине плоскостями. Следовательно, пределы интегрирования по переменной x можно представить как координаты задней и передней границ области. В случае эллипсоида ими будут взятые с отрицательным и положительным знаками величины длин полуоси a : x 1 = − a и x 2 = a .

Таким образом, последовательность интегралов для вычисления объёма эллипсоида следующая:

,

где "игрек первое", "игрек второе", "зет первое" и "зет второе" - полученные выше выражения. Если у Вас есть желание и отвага вычислить этот интеграл и, таким образом, объём эллипсоида, то вот ответ: 4πabc /3 .

Следующие примеры - не такие страшные, как только что рассмотренный. При этом они предполагают не только расстановку пределов интегрирования, но и вычисление самого тройного интеграла. Проверьте, чему вы научились, следя за решением "страшного" примера. Думать при расстановке пределов всё равно придётся.

Пример 6. Вычислить тройной интеграл

если область интегрирования ограничена плоскостями x + y = 1 , x + 2y = 4 , y = 0 , y = 1 , z = 1 , z = 5 .

Решение. "Курортный" пример по сравнению с примером 5, так как пределы интегрирования по "игрек" и "зет" определены однозначно. Но придётся разобраться с пределами интегрирования по "иксу". Проекцией области интегрирования на плоскость xOy является трапеция ABCD .

В этом примере выгоднее проецировать трапецию на ось Oy , иначе, чтобы вычислить тройной интеграл, на придётся разделить фигуру на три части. В примере 4 мы начинали осмотр области интегрирования снизу, и это обычный порядок. Но в этом примере мы начинаем осмотр сбоку или, если так проще, положили фигуру набок и считаем, что смотрим на неё снизу. Можем найти пределы интегирования по "иксу" чисто алгебраически. Для этого выразим "икс" из первого и второго уравнений, данных в условии примера. Из первого уравения получаем нижний предел 1 − y , из второго - верхний 4 − 2y . Сведём данный тройной интеграл к последовательности трёх определённых интегралов:

.

Внимание! В этом примере самый внешний интеграл - не по переменной "икс", а по переменной "игрек", а "средний" - по переменной "икс"! Здесь мы применили смену порядка интегрирования, с которой ознакомились при изучении двойного интеграла. Это связано с тем, что, как уже говорилось, мы начали осмотр области интегрирования не снизу, а сбоку, то есть спроецировали её не на ось Ox , на на ось Oy .

Вычисляем самый внутренний интеграл - по переменной z , считая икс и игрек константами. Получаем:

Вычисляем средний интеграл - по переменной x . Получаем:

.

Наконец, вычисляем самый внешний интеграл - по переменной y :

Ответ: данный тройной интеграл равен 43.

Пример 7. Вычислить тройной интеграл

,

если область интегрирования ограничена поверхностями x = 0 , y = 0 , z = 2 , x + y + z = 4 .

Решение. Область V (пирамида MNRP ) является правильной. Проекцией области V на плоскость xOy является треугольник AOB .

Нижние пределы интегрирования по всем переменным заданы в условии примера. Найдём верхний предел интегирования по "иксу". Для этого выразим "икс" из четвёртого уравнения, считая "игрек" равным нулю, а "зет" равным двум. Получаем x = 2 . Найдём верхний предел интегирования по "игреку". Для этого выразим "игрек" из того же четвёртого уравнения, считая "зет" равным двум, а "икс" - переменной величиной. Получаем y = 2 − x . И, наконец, найдём верхний предел интегрирования по переменной "зет". Для этого выразим "зет" из того же четвёртого уравнения, считая "игрек" и "зет" переменными величинами. Получаем z = 4 − x − y .

Сведём данный тройной интеграл к последовательности трёх определённых интегралов:

.

Вычисляем самый внутренний интеграл - по переменной z , считая икс и игрек константами. Получаем:

.

Вычисляем средний интеграл - по переменной y . Получаем:

.

Вычисляем самый внешний интеграл - по переменной x и окончательно находим данный тройной интеграл:

Ответ: данный тройной интеграл равен 2.

Замена переменных в тройном интеграле и цилиндрические координаты

Если проекцией области интегрирования на какую-либо из координатных плоскостей является круг или часть круга, то тройной интеграл проще вычислисть, перейдя к цилиндрическим координатам. Цилиндрическая система координат является обобщением полярной системы координат на пространство. В системе цилиндрических координат точка M характеризуется тремя величинами (r , φ , z ), где r - расстояние от начала координат до проекции N точки M на плоскость xOy , φ - угол между вектором ON и положительным направлением оси Ox , z - аппликата точки M (рисунок ниже).

Прямоугольные координаты x , y , z с цилиндрическими координатами r , φ , z связывают формулы

x = r cosφ ,

y = r sinφ ,

z = z .

Для того, чтобы в тройном интеграле перейти к цилиндрическим координатам, нужно подынтегральную функцию выразить в виде функции переменных r , φ , z :

То есть переход от прямогольных координат к цилиндрическим осуществляется следующим образом:

Тройной интеграл в цилиндрических координатах вычисляется так же как и в декартовых прямоугольных координатах, путём преобразования в последовательность трёх определённых интегралов:

Пример 8. Вычислить тройной интеграл

переходом к цилиндрическим координатам, где V - область, ограниченная поверхностями и .

Решение. Так как область V на плоскость xOy проектируется в круг , то координата φ изменяется в пределах от 0 до 2π , а координата r - от r =0 до r =1. Постоянному значению в пространстве соответствует цилиндр . Рассматривая пересечение этого цилиндра с областью V , получаем изменение ординаты z от z = r ² до z = 1 . Переходим к цилиндрическим координатам и получаем.